فیزیکدان مشهور اتریشی به نام اروین شرودینگر (Erwin Schrödinger)، نظریه مکانیک کوانتومی را که تازه پای به عرصه نهاده بود به مفید ترین شکل ممکن به علم شیمی و شیمیدانان ارائه نمود. در واقع معادله ذره در جعبه یک معادله موج ریاضی می باشد که در آن چگونگی تغییر حالت کوانتومی یک سیستم فیزیکی را با توجه به زمان نشان می دهد. یکی از معادلات مهم درمکانیک کوانتوم معادلات غیرخطی شرودینگر یا معادله ذره در جعبه می باشد. بررسی سیستم های فیزیکی می تواند به شکل تک ذره ای و یا بس ذره ای انجام گیرد. پاسخ کوآنتومی این نوع از سیستم ها، معمولاً با حل این معادله آغاز می گردد و سرانجام، ادامه کمیات فیزیکی به همراه این پاسخ ها حاصل می گردد. همچنین، محاسبه انرژی های معادله شرودینگر در فیزیک قابل اهمیت است. به عنوان مثال در محاسبه میزان جذب نور.
معادله ذره در جعبه چیست؟
معادلهٔ شرودینگر ، معادلهای است که چگونگی تغییر حالت کوانتومی یک سامانه فیزیکی با زمان را توصیف میکند. این معادله در اواخر سال ۱۹۲۵ فرمول بندی شد و در سال ۱۹۲۶ توسط فیزیکدان اتریشی اِروین شرودینگر منتشر شد.
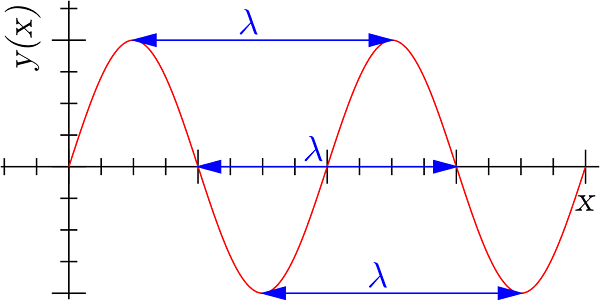
حال که با این دانشمند آشنا شدید، به سراغ معادلهای میرویم که رفتار موجی ذرات را توصیف میکند. به هر ذره با تکانه p، موجی با طولی موج λ نسبت داده میشود. موج مذکور به موج مادی یا «امواج ذرات» معروف است. اروین شرودینگر معادلهای را بر اساس قضیه طول موج دوبروی توسعه داد که موج وابسته به ذرات و چگونگی تغییر حالت سیستمهای کوانتومی را توصیف میکند.
بررسی اثر معادله شرودینگر
از مکانیک کلاسیک میدانیم که در بررسی حرکت ذره ابتدا معادله حرکت آن ذره را پیدا میکنند و بر اساس آن در مورد چگونگی حرکت بحث میکنند. میدانیم که در مکانیک کوانتومی ، بر اساس نظریه دوبروی در مورد ذرات دو دیدگاه موجی و ذرهای در نظر گرفته میشود و اصل مکملی نور مانع از این میشود که این دو تصویر را به صورت همزمان بکار ببریم. ولی برای توصیف کامل حرکت ، هر دو دیدگاه باید در نظر گرفته شوند. بر این اساس معادلهای که به حرکت این ذرات کوانتومی حاکم است، معادله شرودینگر نامیده میشود.
حرکت ذره آزاد در معادله شرودینگر
معمولا سادهترین حالت در مکانیک کوانتومی حرکت یک ذره آزاد است. لفظ آزاد به این لحاظ بکار میرود که این ذره تحت تاثیر هیچ پتانسیلی قرار ندارد. در این صورت معادله شرودینگر در مورد حرکت ذره مورد نظر ، با این فرض که حرکت در یک بعد صورت میگیرد، به صورت زیر خواهد بود:
![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4894f9a205c471cb012351a1fccdd01285b6f11c)
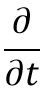
رابطه فوق m جرم ذره ، h ثابت پلانک ، Ψ تابع موجی است که در تشریح دیدگاه موجی ، به ذره مورد نظر نسبت داده میشود. همچنین i یک واحد موهومی است که مجذور آن برابر (1-) میباشد (عدد مختلط). در این رابطه نماد
بیانگر مشتق نسبی نسبت به زمان و نشانگر مشتق نسبی نسبت به مکان است.
خصوصیات معادله شرودینگر
- معادله شرودینگر نسبت به مشتق زمان از مرتبه اول است. این امر ایجاب میکند که وقتی مقدار اولیه تابع موج منتسب به ذره ، به عنوان مثال در لحظه t=0 معلوم باشد، مقدار آن را در هر لحظه دیگر نیز بتوان پیدا کرد. خب این مطلب از شکل این معادله ، یا از شکل عمومیترین جواب این معادله ، که یک رابطه انتگرالی است، مشهود است.
- نکته دیگر این است که در معادله شرودینگر هیچ عدم قطعیتی وجود ندارد. به بیان دیگر ، همین که حالت اولیه تابع موج مشخص شد، در این صورت در هر زمان دیگری ، آن تابع موج کاملا مشخص میگردد. دلیل این مطلب در اینجاست که هیچ محدودیتی بر روی تابع موج حالت اولیه وجود ندارد.
3 کاربرد معادله ذره در جعبه
- با استفاده از حل معادله شرودینگر مشخصههای سیستم از قبیل ترازهای انرژی اندازه حرکت خطی و اندازه حرکت زاویه ای سیستم مشخص میشود.
- از حل معادله شرودینگر تابع موج منتسب به هر سیستم فیزیکی بدست میآید. با استفاده از تابع موج میتوان چگالی احتمال را محاسبه نموده و حرکت ذرات سیستم را مورد بررسی قرار داد.
- برای هر سیستم این معادله مخصوصی وجود دارد که وابسته به هامیلتونی تعریف شده برای آن سیستم است.
مطالب فوق جهت اطلاعات رسانی به شما درج شده است. برای درک بیشتر و آموزش کافی از مفهوم این بخش به تماشای ویدئوی زیر بنشینید و در پایان هرگونه سوال و مطلبی برای بیان داشتید، در پایین پیج ذکر کنید. در اسرع وقت به سوالات شما پاسخ داده خواهد شد.




